Quadratics

Quadratic Formula: The Discriminant

 

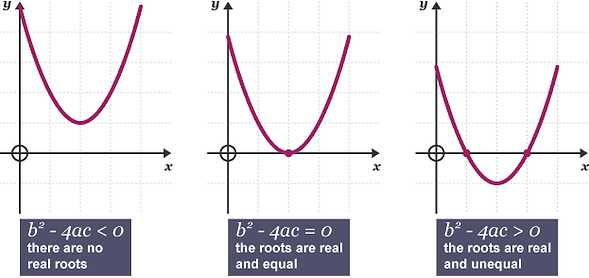
Throughout this section, we will be further exploring the "quadratic formula". More specifically, we will be looking at the "discriminant". The "discriminant" is the value inside of the square root. The "discriminant" can very useful in this unit because it can tell us if the equation has either one root, two distinct roots, or no real root at all. One key thing to remember is that in order to use the discriminant, you need the equation equal to 0. 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

From the graphic located above, we can see that the value of b^2-4ac in the "quadratic formula" is the discriminant. This value may also be commonly referred to as D. As mentioned earlier on, the discriminant helps us tell how many solutions (roots) a quadratic equation has. 

 

 

Number of Solutions and Discriminants:

 

CASE A: For equations with the property D=O, there is only one real root/solution. 

CASE B: For equations with the property D>0, there are two real roots/solutions.

CASE C: For equations with the property D<0, there are no real roots/solutions. 

 

*Below are graphs that show each of the listed properties of the discriminants.