Investigating Vertex Form
Throughout the quadratics unit, there are three forms we will be talking about: vertex form, factored form, and the standard form. In this section, we will be specifically focusing on investigating the vertex form. Please take a look below and locate the vertex form equation, as we will be using it as a starting point in investigating the vertex form.
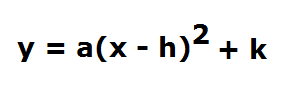
PART A: Exploring the effect of a in y= a(x-h)^2+k
The a-value is responsible for deciding whether your parabola would undergo a "vertical stretch" or a "vertical compression". If a>1 , then it would yield a "vertical stretch". However, if -1<a>1, then it would yield a "vertical compression". Not only does the a-value tells us whether the parabola underwent a "vertical stretch" or "vertical compression", it also tells us whether the parabola would open upwards or downwards. If the a-value is positive, then the parabola would open upwards. However, if the a-value is negative, the parabola would open downwards.
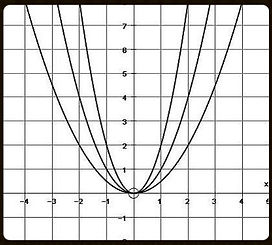
Vertical Stretch
Original
Vertical Compression
PART B: Exploring the effect of h in y= a(x-h)^2+k
The h-value is responsible for deciding the "horizontal shift" of the parabola. It only affects the x-values, as it only moves the parabola along the x-axis. *This value is ALWAYS the opposite of the h-value stated in the vertex form equation.*
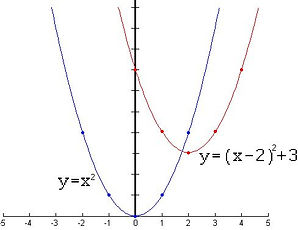
From this graph, we notice that the equation for the parabola in red is y=(x-2)^2+3. However, if we closely observe the graph, we can see that the parabola in red (to which the above equation applies to) is shifted two units to the right (in the positive direction). In the example above, the h-value was negative in the vertex form equation. However, when it came time to graph the parabola, instead of shifting two units to the left, the graph shifted two units to the right (in the positive direction). Therefore, from this graph we can conclude, that the h-value is always opposite to the value stated in the vertex form equation.
PART C: Exploring the effect of k in y= a(x-h)^2+k
The k-value is responsible for deciding the "vertical shift" of the parabola. It only affects the y-values, as it only moves the parabola along the y-axis. If the k-value is positive, then the parabola would move upwards. However, if the k-value is negative, the parabola would move downwards.
*If visual diagram is required for understanding the effects of k in a vertex form equation, please refer to the diagram above.
