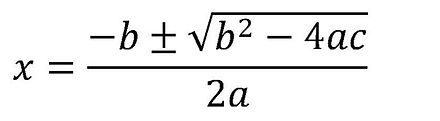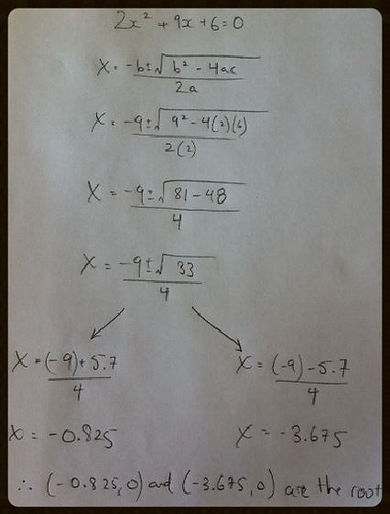Quadratics

Quadratic Formula

 

Throughout this section, we will be learning about the "quadratic formula". This formula will prove to be very useful when working with equations in standard form. This is because when this formula is applied to an equation in standard form, one is able to very easily find the     x-intercepts (roots) of the relation. Furthermore, it is also very easy to work with equations in standard form because you can literally take the values from the equation, and plug it into the quadratic formula to find your x-intercepts. Whenever you cannot factor an equation to solve for its x-intercepts, the quadratic formula proves to be very useful. Please look below to see the formula itself: 

 

 

 

 

 

 

 

 

 

 

Now that we know the "quadratic formula", let us examine how to use it with an equation in standard form to find its x-intercepts (roots). Please take a look at the example below to see how this formula is applied:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

In the sample problem above, the value of the equation was set to O. Hence, it was much simpler to apply the formula. However, the equation is not always going to be equal to 0. Sometimes, the value may be greater than 0. In that case, there is an additional step involved. If the equation is equal to a value greater than 0, then you have to bring the value to the side with all the other terms, and then simplify. Now, you have made the equation equal to 0. From there on, you apply the quadratic formula and solve for the possible roots of the relation. 

 

 

*Now that you know the formula, and how to apply it to solve for the roots, it is time for practice. Please visit the link below and complete the given problem sheet:

URL: http://cdn.kutasoftware.com/Worksheets/Alg1/Quadratic%20Formula.pdf